Konsep dan 6 Sifat Pembagian Bilangan Bulat, Contoh Soal dan Pembahasan
- Get link
- X
- Other Apps
Misalkan kamu memiliki 10 buah jeruk yang akan kamu bagikan sama rata kepada 5 orang teman kamu. Pertanyaannya, berapakah jumlah jeruk yang diterima oleh masing-masing temanmu? Tentunya masing-masing temanmu akan mendapat 2 buah jeruk. Nah, peristiwa tersebut merupakan salah contoh bentuk pembagian bilangan bulat. Lalu tahukah kamu bagaimana konsep dan sifat-sifat pembagian bilangan bulat? Untuk menjawab pertanyaan tersebut, silahkan simak secara seksama penjelasan berikut ini.
Misalnya pada suatu saat kalian ditanya, “Berapakah nilai a yang memenuhi persamaan 42 : 7 = a?” Dan pada saat yang lain kalian ditanya lagi, “Bilangan berapakan yang dikalikan dengan 7 menghasilkan bilangan 42?” Dari contoh soal ini, apakah keduanya memiliki jawaban yang sama? Kedua soal ini apabila disederhanakan, maka bentuknya adalah seperti berikut.
42 : 7
|
=
|
a
|
a × 7
|
=
|
42
|
Ternyata, nilai a yang memenuhi jawaban kedua persamaan di atas adalah 6. Lalu apa yang dapat kamu simpulkan dari kedua bentuk pertanyaan tersebut? Operasi pembagian bilangan bulat merupakan kebalikan dari operasi perkalian, sehingga dapat disimpulkan sebagai berikut.
Jika a, b, dan c adalah bilangan bulat dan b ≠ 0 maka a : b = c jika dan hanya jika a = b × c.
|
Operasi pembagian bilangan bulat dapat dinyatakan dalam beberapa bentuk, di antaranya adalah sebagai berikut.
Bentuk pembagian di atas dapat digunakan sesuai dengan kebutuhan. Bentuk 148 : 4 digunakan untuk pembagian yang sederhana, sedangkan bentuk 3426 biasanya digunakan untuk pembagian yang rumit. Ada beberapa istilah yang perlu diketahui dalam operasi pembagian bilangan bulat, yaitu pembagi, bilangan yang dibagi, hasil bagi, dan sisa pembagian. Agar lebih jelas, perhatikan contoh berikut ini.
Mengingat pembagian merupakan kebalikan dari perkalian, maka dapat dituliskan sebagai berikut.
a × b = c ⇔ c : a = b atau c : b = a
Sekarang coba kalian perhatikan tabel berikut!
a × b = c
|
c : a = b
|
c : b = a
|
3 × 4 = 12
|
12 : 3 = 4
|
12 : 4 = 3
|
3 × (−4) = −12
|
−12 : 3 = −4
|
−12 : (−4) = 3
|
−3 × 4 = −12
|
−12 : (−3) = 4
|
−12 : (4) = −3
|
−3 × (−4) = 12
|
12 : (−3) = −4
|
12 : (−4) = −3
|
Dari data-data perhitungan pada tabel di atas, maka dapat kita ambil beberapa pola tanda pada pembagian bilangan bulat berikut ini.
a. (+) : (+) = (+)
b. (+) : (−) = (−)
c. (-) : (+) = (−)
d. (−) : (−) = (+)
Dengan demikian dapat kita simpulkan konsep dari pembagian bilangan bulat yaitu sebagai berikut,
■
|
Hasil bagi dua bilangan bulat yang mempunyai tanda sama selalu positif.
|
■
|
Hasil bagi dua bilangan bulat yang mempunyai tanda berbeda selalu negatif.
|
Sifat-Sifat Pembagian Bilangan Bulat
Sifat-sifat pembagian bilangan bulat antara lain tidak tertutup, tidak komutatif, tidak asosiatif, tidak distributif, pembagian bilangan bulat dengan nol (0), dan pembagian bilangan bulat oleh nol. Berikut ini adalah penjelasan dan contoh masing-masing sifat tersebut.
#1 Tidak Bersifat Tertutup
Sifat tertutup adalah sifat operasi hitung pada bilangan bulat yang menghasilkan bilangan bulat juga, perhatikan contoh berikut:
Contoh:
● 15 : 3 = 5
15 dan 3 merupakan bilangan bulat, hasilnya yaitu 5 juga merupakan bilangan bulat. Sekarang coba kalian perhatikan contoh berikutnya.
● 4 : 3 =?
Berapakah hasil pembagian antara 4 dengan 3? Apakah kalian menemukan nilai dari 4 : 3 merupakan bilangan bulat? jawabannya adalah tidak ada. Karena tidak ada bilangan bulat yang memenuhi, maka hal ini sudah cukup untuk menyatakan bahwa pembagian pada bilangan bulat tidak bersifat tertutup. Dengan demikian, dapat kita tuliskan sebagai berikut.
Untuk setiap bilangan bulat a dan b, jika a : b = c, maka c belum tentu merupakan bilangan bulat.
|
#2 Tidak Bersifat Komutatif
Untuk memahami sifat tidak komutatif atau anti komutatif pada pembagian bilangan bulat, perhatikan contoh berikut ini.
Contoh:
● 20 : (−10) = −2
● −10 : 20 = −0,5
Dengan demikian, 20 : (−10) ≠ −10 : 20 sehingga pada pembagian bilangan bulat tidak berlaku sifat komutatif. Secara umum dituliskan sebagai berikut.
Hasil pembagian bilangan bulat tidak pernah sama ketika letak bilangan ditukar. Sifat pembagian seperti ini disebut sifat anti komutatif dan ditulis sebagai berikut:
a : b ≠ b : a
|
#3 Tidak Bersifat Asosiatif
Untuk memahami sifat anti asosiatif pada pembagian bilangan bulat, perhatikan contoh di bawah ini.
Contoh:
● (12 : 6) : 2 = 2 : 2 = 1
● 12 : (6 : 2) = 12 : 3 = 4
Dengan demikian, (12 : 6) : 2 ≠ 12 : (6 : 2) sehingga pada pembagian bilangan bulat tidak berlaku sifat asosiatif. Secara umum dituliskan sebagai berikut.
Hasil pembagian bilangan bulat tidak pernah sama ketika elemen-elemennya dikelompokkan dengan cara yang berbeda. Sifat pembagian seperti ini disebut sifat anti asosiatif dan ditulis sebagai berikut:
(a : b) : c ≠ a : (b : c)
|
#4 Tidak Bersifat Distributif
Untuk memahami sifat anti distributif pada pembagian bilangan bulat, perhatikan contoh di bawah ini.
Contoh:
Pada penjumlahan
● 30 : (10 + 5) = 30 : 15 = 2
● (30 : 10) + (30 : 5) = 3 + 6 = 9
Pada pengurangan
● 20 : (10 − 5) = 20 : 5 = 4
● (20 : 10) – (20 : 5) = 2 – 4 = –2
Dengan demikian, 30 : (10 + 5) ≠ (30 : 10) + (30 : 5) dan 20 : (10 − 5) ≠ (20 : 10) – (20 : 5) sehingga pada pembagian bilangan bulat tidak berlaku sifat distributif baik pada penjumlahan maupun perkalian. Secara umum dituliskan sebagai berikut.
Pada operasi pembagian bilangan bulat, tidak berlaku sifat distributif (penyebaran). Secara umum, untuk a, b dan c bilangan bulat, maka
■ a : (b + c) = (a : b) + (a : c)
■ a : (b − c) = (a : b) − (a : c)
|
#5 Pembagian Bilangan Bulat dengan Nol
Misalkan 5 : 0 = p ⇔ 0 × p = 5
Tidak ada satupun pengganti p pada bilangan bulat yang memenuhi 0 × p = 5, sehingga dapat disimpulkan bahwa:
Untuk setiap bilangan bulat a, a : 0 tidak terdefinisi.
|
#6 Pembagian Bilangan Bulat oleh Nol
Untuk pembagian 0 : 3 = n, adakah pengganti n yang memenuhi? Perhatikan uraian berikut ini.
0 : 3 = n ⇔ 3 × n = 0
Pengganti n yang memenuhi 3 × n = 0 adalah 0. Jadi, kesimpulannya adalah sebagai berikut.
Untuk setiap bilangan bulat a, berlaku 0 : a = 0.
|
Contoh Soal dan Pembahasan
Agar kalian dapat memahami konsep dan sifat-sifat operasi pembagian pada bilangan bulat, silahkan pelajari beberapa contoh soal dan penyelesaiannya berikut ini.
Contoh Soal #1
Tentukan hasil pembagian bilangan bulat berikut ini.
a. 90 : 5
b. –108 : (–18)
b. 56 : (–8)
c. –84 : 7
d. 51 : (–3)
e. –72 : 4
f. 52 : 0
g. 0 : (–49)
h. –64 : (–8)
i. 128 : (–8)
Jawab:
a. 90 : 5 = 18
b. –108 : (–18) = 6
b. 56 : (–8) = –7
c. –84 : 7 = –12
d. 51 : (–3) = –17
e. –72 : 4 = 18
f. 52 : 0 = tidak terdefinisi
g. 0 : (–49) = 0
h. –64 : (–8) = 8
i. 128 : (–8) = –16
Contoh Soal #2
Tentukan hasil pembagian berikut (jika ada bilangan bulat yang memenuhi).
a. 72 : 6
b. –30 : (–6)
c. 52 : 3
d. 82 : –9)
e. –70 : 4
f. –96 : (–18)
Jawab:
a. 72 : 6 = 12
b. –30 : (–6) = 5
c. 52 : 3 = tidak ada bilangan bulat yang memenuhi
d. 82 : (–9) = tidak ada bilangan bulat yang memenuhi
e. –70 : 4 = tidak ada bilangan bulat yang memenuhi
f. –96 : (–18) = tidak ada bilangan bulat yang memenuhi
Contoh Soal #3
Tentukan pengganti nilai m, sehingga pernyataan berikut menjadi benar.
a. m × (–4) = –88
b. 9 × m = –54
c. m × (–7) = 91
d. m × (–13) = –104
e. –16 × m = 112
f. 8 × m = –136
g. m × 12 = 156
h. m × (–6) = –144
Jawab:
a. m = –88 : (–4) = 22
b. m = –54 : 9 = –6
c. m = 91 : (–7) = –13
d. m = –104 : (–13) = 8
f. m = –136 : 8 = –17
g. m = 156 : 12 = 13
h. m = –144 : (–6) = 24
- Get link
- X
- Other Apps
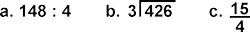



Comments
Post a Comment
Mohon berkomentar secara bijak dengan bahasa yang sopan dan tidak keluar dari topik permasalahan dalam artikel ini. Dan jangan ikut sertakan link promosi dalam bentuk apapun.
Terimakasih.